C#数据结构与算法 --- 排序算法（三）

引言

上一篇数据结构与算法 --- 排序算法（二）中，介绍了分治算法思想及借助分治算法思想实现的归并排序。

本篇来讲解一下快速排序，它也是借助分治算法思想实现，但其处理思路与归并排序完全不一样。

快速排序

来看一下快速排序的算法原理：.

算法图解

如果要排序数组中 p 到 r 的数据，那么，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点），然后遍历从 p 到 r 的数据，将小于 pivot 的放到左边，将大于或等于 pivot 的放右边，将 pivot 放中间，经过这一步骤处理之后，从 p 到 r 的数据就被分成了3部分。

假设 pivot 现在的位置下标是 q，那么从 p 到 q-1 的数据都小于 pivot，中间是 pivot，从q+1 到 r 都是大于 pivot，如下图：

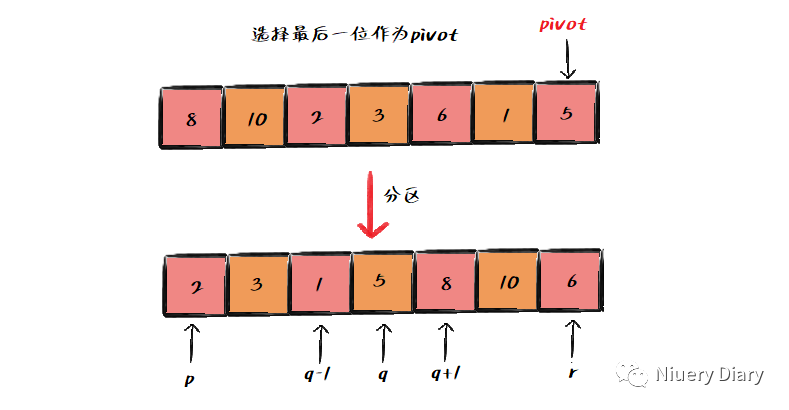
根据分治的处理思想，分区完成之后，开始递归下标从 p 到 q-1 的数据和下标 q+1 到 r 的数据，知道待排序区间的大小缩小为1，就说明数据都有序了。

如果使用递推公式将上面的过程表示出来，递推公式：

终止条件：

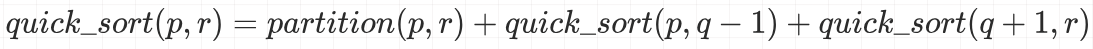
C#数据结构与算法 --- 排序算法（三）

终止条件：p >= r

其中 partition() 分区函数要做的就是随机选择一个元素作为 pivot（一般选择 p到r区间中的最后一个元素），然后基于 pivot 对区间 Arr[p,r] 进行分区，分区函数返回分区之后的 pivot 的下标。

使用c#代码实现如下：

classQuickSort
{
    public static void Sort(int[] arr)
    {
        if (arr == null || arr.Length == 0)
            return;

        QuickSortRecursive(arr, 0, arr.Length - 1);
    }

    private static void QuickSortRecursive(int[] arr, int left, int right)
    {
        if (left >= right)
            return;

        int pivotIndex = Partition(arr, left, right);
        QuickSortRecursive(arr, left, pivotIndex - 1);
        QuickSortRecursive(arr, pivotIndex + 1, right);
    }

    private static int Partition(int[] arr, int left, int right)
    {
        //这里可以选择不同的策略，比如随机数选取或选择中间值
        int pivotIndex = ChoosePivot(left, right);
        int pivotValue = arr[pivotIndex];
        Swap(arr, pivotIndex, right);

        int currentIndex = left;
        for (int i = left; i < right; i++)
        {
            if (arr[i] < pivotValue)
            {
                Swap(arr, i, currentIndex);
                currentIndex++;
            }
        }

        Swap(arr, currentIndex, right);
        return currentIndex;
    }

    private static int ChoosePivot(int left, int right)
    {
        //这里选择使用中间值
        return (left + right) / 2; 
    }

    private static void Swap(int[] arr, int i, int j)
    {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

算法分析

「内存消耗」：

如果不考虑空间消耗的话，那么 partition() 分区函数实现非常简单，直接申请两个临时数组 X 和 Y，遍历目标区间 Arr[p,r] ，小于 pivot 的直接复制到X，大于pivot的直接复制到Y，最后按顺序将X，pivot，Y依次复制到目标区间 Arr[p,r]。

但是，如果这样实现的话， partition() 执行的过程中将消耗很多额外内存空间，快速排序也就不是原地排序算法了，如果希望快速排序是原地排序算法，该怎么做呢？

这就需要之前文章中提到的「通过交换来避免搬移」，具体实现类似选择排序，通过游标 i 把Arr[p,r-1] 分成两个部分，Arr[p,i-1] 的元素都小于 pivot (也就是Arr[r])，暂且称之为“已处理区间”，对应的，Arr[i,r-1] 是“未处理区间”。每次从未处理区间 Arr[i,r-1] 中取出一个元素Arr[j] 与 pivot 对比，如果小于 pivot，则将其插入到已处理区间的尾部，也就是下标为 i 的位置。具体图解可以参考数据结构与算法 --- 排序算法（一）中的选择排序算法图解。

「稳定性」：

理解完了快速排序是原地排序算法，那么分析一下该排序算法是否稳定排序？

其实也很简单，排序算法涉及到了分区，分区的操作实现又是按照选择排序原理实现，选择排序本身就是不稳定排序算法，所以快速排序也是不稳定排序。

「时间复杂度」：

最好情况时间复杂度：O(nlogn)

在最好的情况下，快速排序的时间复杂度为 O(nlogn)。这种情况发生在每次划分时，待排序数组恰好被平均地分成两个大小相近的子数组。此时，快速排序的递归树的深度较小，每一层的时间复杂度为 O(n)，总的时间复杂度为 O(nlogn)。
最坏情况时间复杂度：O(n²)

在最坏的情况下，快速排序的时间复杂度为 O(n²)。这种情况发生在每次划分时，待排序数组中的元素都被划分到了同一侧，导致一侧的子数组非常大，另一侧为空。这样就会导致快速排序的递归树非常不平衡，每一层的时间复杂度为 O(n)，而递归的层数为n，因此总的时间复杂度为 O(n²)。
平均情况时间复杂度：O(nlogn)

在平均情况下，快速排序的时间复杂度为 O(nlogn)。快速排序采用分治策略，在平均情况下，待排序数组会被平均地划分成两个大小相近的子数组，这样递归树会相对平衡，每一层的时间复杂度为 O(nlogn)，总的时间复杂度为 O(nlogn)。

总结

需要注意的是，快速排序的性能高度依赖于划分元素的选择。在实际实现中，通常会采取一些优化措施，如三数取中法或随机选取划分元素，以尽量避免最坏情况的发生。总体来说，快速排序在大多数情况下表现良好，因为平均时间复杂度为O(nlogn)，它是一种快速且高效的排序算法。

引言

快速排序

算法图解

算法分析

总结

董川民